目次 [ Contents ]
Arduinoでプログラミングを学習していく過程で、最初は分からなかったけど、他の理解が進んでから見直すと意外に簡単に呑み込めたりすることがあります。16進数に関しても、最初わけ分からんと放置してました。ところがやりたい事が増えると、どうしてもその避けてきたことが必要になって、学習せざるを得なくなり…。ただ、以前は16進数を使う利点がよく呑みこめず受けつかなかったわけで、それが分かると割と楽に理解できたように思います。
ということで、その辺に気を配りつつ、16進数について書いてみたいと思います。僕のように毛嫌いしている方も、これを読んで前向きになって頂ければ。
16進数 Hexadecimal
16進数とは
「数を16進数で表記すること」です。英語でHexadecimalと書きます。6(Hexa)と10の進数(decimal)でHexadeciminalです。略してHEXと書いてたりします。
では16進数とはどういうものなのか。
日常使っている数字は10進数です。数字の9の次は10ですよね。これは「10」で桁が一つ繰り上がることを意味します。つまり、16進数は「16」で桁が繰り上がる表示方法です。
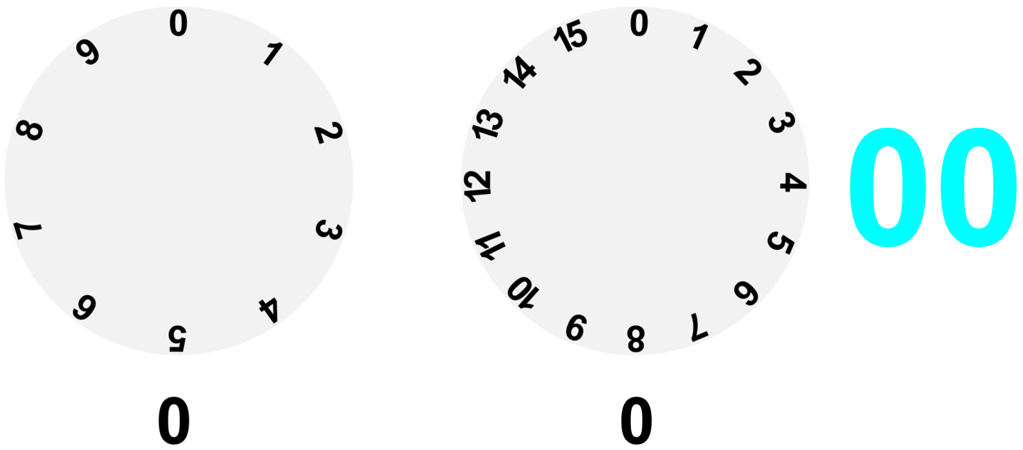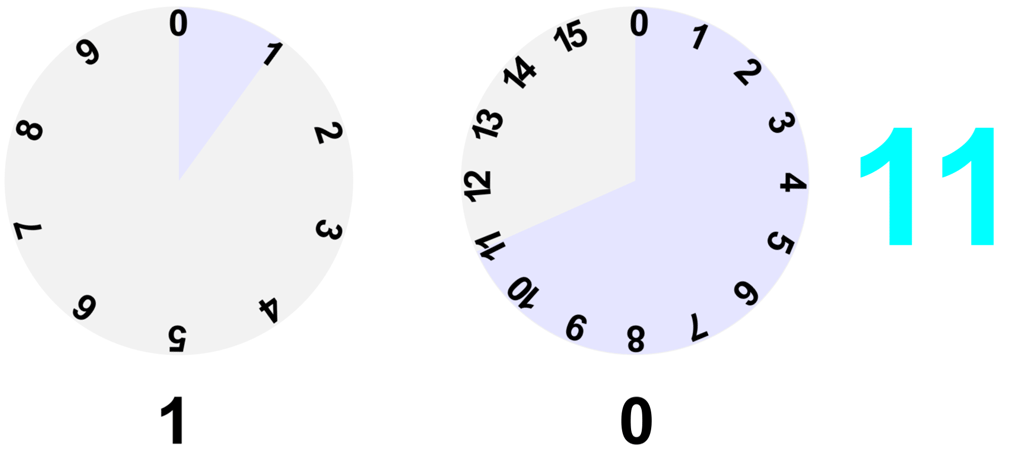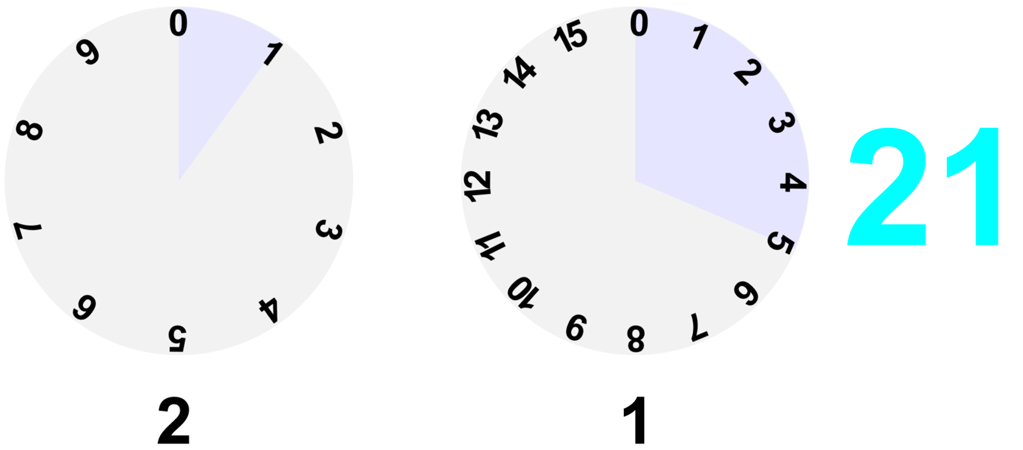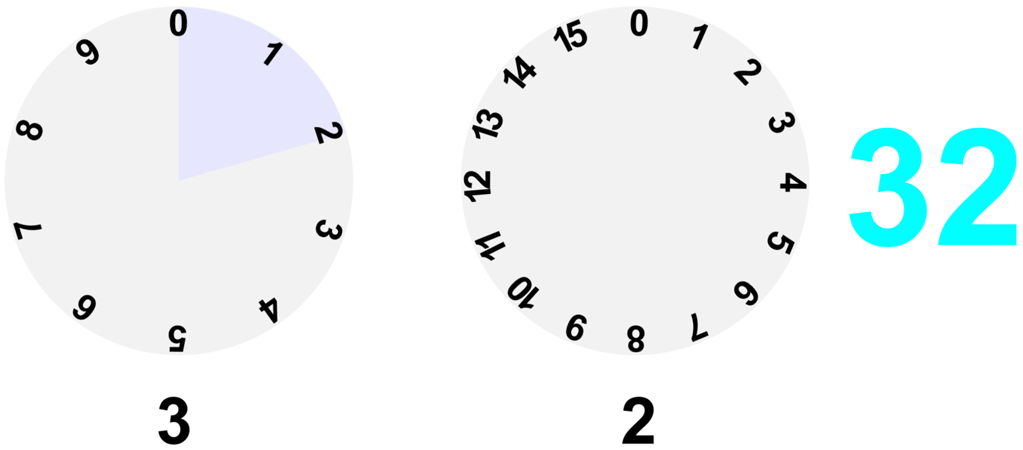
面倒臭そうで実際面倒なんですけど、実はこういった変換をみんな日常的にやっています。例えば時間。時間は60進数であり、60秒で1分、60分で1時間とカウントしてますね。これと一緒です(実際は60時間の次は61時間だし、1秒の下は999ミリセコンドという中途半端な60進数ですが…)あとはダースとか。世の中には10コ単位で区切らない数え方はよくあります。
21時間43分を秒数で表せと言われたら面倒なのと一緒で、16進数も難しくはないけど面倒さがつきまといます。でも、時間の計算ができるなら16進数の計算もそこまで難解ではない筈です。
表記の仕方
一般的に使われている10進法では0から9の文字を組み合わせて表現しています。「9」の次は繰り上がって1と0になるので「10」。つまり10個文字があれば全ての数字を表現出来るわけです。
でも、16進数は「16」で繰り上がるので、さらに6つ文字が必要になります。10〜15に当たる文字を考えてもいいですが、世間ではもっと単純にアルファベットが使用されています。つまり、
となります。普段扱っている10進数の数を16進数で表すと、
| 10進数 | 16進数 | 16進数の構成 | |
| 5 | = | 5 | 5 |
| 15 | = | F | 15 |
| 16 | = | 10 | 16 * 1 + 0 |
| 17 | = | 11 | 16 * 1 + 1 |
| 80 | = | 50 | 16 * 5 + 0 |
| 160 | = | A0 | 16 * 10 + 0 |
16進数だと大きな数字ほど少ない文字で表示できる利点があります。ただ、桁が増えるとどんどん面倒な感じになってきます。16が「10」、80が「50」っていうのも紛らわしいですよね。
実際コンピュータの世界では間違いを防ぐために16進数での数字表現は頭に「0x」という文字を足し、偶数の桁数で表現をしています。
| 10進数 | 16進数 | |
| 15 | = | 0x0F |
| 16 | = | 0x10 |
| 80 | = | 0x50 |
変換計算
16進数を10進数へ
2桁目以上の数は16の累乗を掛けていきます。例えば「0x0ABC」という数があったら、
| 4桁目 | 3桁目 | 2桁目 | 1桁目 | |
| 16進数 | 0 | A | B | C |
| 10進数 | 0 | 10 | 11 | 12 |
それぞれの位の数に16の累乗を掛けていき、合計をとります。
| 位 | 16進数 | 計算 | 各位の答 | |
| 1桁目 | 1の位 | C | 12 | 12 |
| 2桁目 | 16の位 | B | 11*16 | 176 |
| 3桁目 | 256の位 | A | 10*16*16 | 2560 |
| 4桁目 | 4096の位 | 0 | 0*16*16*16 | 0 |
| 合計 | 2748 |
やること自体は単純ですが中々、気が滅入る計算です。
10進数だと位は0が増えるだけなんですが、16進数は中途半端な位の上がり方なので、こう厄介になります。
10進数を16進数へ
16進数への変換は、逆に16で割っていき、余りを出していきます。それが位の数字になります。「2748」という10進数を例にすると、
| 数字 | 答え | 余り | (余りの)16進数 | ||
| 1回目 | 2748 | ÷16 | 171 | 12 | C |
| 2回目 | 171 | ÷16 | 10 | 11 | B |
| 3回目 | 10 | ÷16 | 0 | 10 | A |
| 合計 | 0x0ABC |
難しい話ではないけど、これもまた非常に面倒です。
16進数は必要?
計算が嫌いな人間にとって、こういった作業は苦痛でしょうがないんですが、果たしてこんな面倒な手続きは常に必要なんでしょうか?
大きな数字を右から左へ受け流すだけなら、答えは「NO」です。面倒な計算をしていちいち変換する必要はありません。プログラミング上で勝手に変換してくれるし、Serial.printではフォーマット変換する引数も用意されています。そもそも表示の仕方が違うだけの話であって、結果には何の影響もありません。0xA0個のうまい棒と、160個のうまい棒を買うのにかかる値段は一緒ですから。
ただし、2桁の16進数が理解できると、後々スケッチの書き方や理解に大きい差が出てきます。
ByteとHEX
16進数の解読が必要になってくるのは、通信プロトコルの制御や、ビット操作をするようになってからです。例えばI2Cでディスプレイに何かコマンド出したいとか、SPIで他のデバイスとやりとりしたいとか。そんな時、世の中のByteデータは、大抵HEXで表示されてます。
ではそのHEXについて、と言いたいとこですが、その前にbit、つまり2進数を理解している必要が出てきます。
bitとByte
コンピュータ上でのデータの最小単位はbitです。電圧があるかないか、YesかNoか、1か0か。それが1bitです。しかし、このままでは1個の判別しかできません。が、これを8回ひとくくりで考えることで0〜255の256個の判別が可能になります。それが1Byte(8bit)であり、デジタル、コンピュータの基本になります。
| bit数 | 10進数 | 2進数 |
| 1 | 0 | B0 |
| 1 | B1 | |
| 2 | 2 | B10 |
| 3 | B11 | |
| 3 | 4 | B100 |
| 5 | B101 | |
| 6 | B110 | |
| 7 | B111 | |
| 4 | 8 | B1000 |
| ~ | ||
| 8 | 254 | B11111110 |
| 255 | B11111111 |
この0と1の文字だけで数字を表示する方法が2進数で、bitでの表示の場合は頭に「B」をつけます。混乱を避けるため「0x」をつける16進数と同じ考えです。
それにしても2進数で大きい数字を読み書きするのは紛らわしくて、かなり大変ですよね。2進数も16進数の時のように通常ではあまり関わりたくありません。
が、実際はスケッチを簡潔に書くためによく利用されます。というか良くできたプログラミングほど2進数で無駄のないやりとりとしています。最小単位で扱えるからです。なので、複雑なことを理解したり、やってみようとすれば、この理解は必然になってきます、残念ながら。
10進数を2進数へ
例えば「218」という数字があったとして、これを2進数にするには下記の表を利用します。
| 8bit目 | 7bit目 | 6bit目 | 5bit目 | 4bit目 | 3bit目 | 2bit目 | 1bit目 |
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
8bitだと255まで表現できますが、「218」という数字をこの表の組み合わせだけで表現できるよう模索します。つまり、218 = 128+64+16+8+2というのを割り出します。すると、
| 8bit目 | 7bit目 | 6bit目 | 5bit目 | 4bit目 | 3bit目 | 2bit目 | 1bit目 |
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
使っている桁を(1)に、それ以外を(0)にすれば、そのまま2進数になるわけです。
| 10進数 | 2進数 |
| 218 | B11011010 |
逆に10進数への変換は1になっている桁の数字を全部抜き出して足せばいいだけです。
128+64+16+8+2、やってきた工程を戻るだけですね。
しかしながら、やはり2進数は煩わし過ぎてあまり数えたくない表記です。
そこで16進数が出てきます。HEXで表示しておくことで、そこら辺がスッキリしてきます。
ByteをHexで表示
とりあえずB11011010(218)をHEXへ変換します。
16進数にするにはまず便宜上4つごと、4bitに区切ります。すると4bitで表現できるのは0〜15。つまり4bitなら16進数1文字で表記出来ます。
| 2進数 | B11011010 | |
| 4bitづつに分割 | B1101 | B1010 |
| 10進数 | 13 | 10 |
| 各位のHEX表記 | D | A |
| 16進数 | 0xDA | |
意外に単純な話ですよね。Byteの数値はこうやって16進数で表現されています。
実は、こう16進数で表記することで2進数への変換がとても楽になります。また、計算は必要ですが、10進数へも変換できます。つまり橋渡し役として勝手がいいわけです。
1ByteのHEXを10進数へ
2桁の16進数を10進数にするなら上の位に16を掛けます。あとは下の位と足します。0xDAなら、
D * 16 + A = 13 * 16 + 10 = 218
1ByteのHEXを2進数へ
2進数へ変換するには前述の表を4bit分だけ覚えるだけで済みます。求める数字は8、4、2、1をどう足せば揃うのかを探すだけです。
例えば10進数の「11」から2進数を求めるなら、11 = 8+2+1なので、
| 4bit目 | 3bit目 | 2bit目 | 1bit目 |
| 8 | 4 | 2 | 1 |
| 1 | 0 | 1 | 1 |
10進数「11」の2進数は「B1011」ということになります。
10進数「218」から直接2進数を求めようとすると、8bitの表を利用して探すので、ちと面倒ですが、「0xDA」という16進数からであれば、
| D(13) | A(10) | |||||||
| 構成数 | 8+4+1 | 8+2 | ||||||
| 各位bitの最大値 | 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 |
| 2進数 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
B11011010が楽に求められます。
4bitづつに分けて計算できることで、簡単さが全然違ってきます。更に言うと16進数なら1Byte以上であっても変換がしやすくなります。
例えば2Byteの「0xD8F2」なら、
| 各位16進数 | D | 8 | F | 2 |
| 各位10進数 | 13 | 8 | 15 | 2 |
| 各位構成 | 8+4+1 | 8 | 8+4+2+1 | 2 |
つまり、
| 16進数 | D | 8 | F | 2 |
| 10進数 | 13 * 16 * 16 * 16 | 8 * 16 * 16 | 15 * 16 | 1 |
| 2進数 | 1101 | 1000 | 1111 | 0010 |
10進数:53248 + 2048 + 240 + 2 = 55538
2進数 :B1101100011110010
10進数への変換はさすがに電卓が欲しいですが、16進数で表示されていることで、何かと勝手が良いのが分かります。文字数も簡潔だし。
この仕組みが分かれば、パーツのデータシートも何となく理解できるようになってくるかと思います。例えば、液晶に送るコマンドとか。
秋月電子 8×2キャラLCD
変換の練習
一通り説明してきましたが、結局10進数と2進数の変換に慣れないとHEXを扱いづらいところがあります。以前も書きましたが、そういう練習はゲームで覚える楽でいいですよ。

